Giải mã thành công câu đố Descartes sau 380 năm chờ đợi
Định lý Descartes đã trở thành một trong những định lý nổi bật trong lịch sử toán học, không chỉ vì những câu hỏi lý thuyết mà nó đặt ra mà còn do những tác động mạnh mẽ của nó đến các lĩnh vực nghiên cứu hiện đại. Bài viết này sẽ giải mã những tiến bộ gần đây trong nghiên cứu Định lý Descartes từ Đại học Monash, khám phá sự kết hợp giữa toán học và vật lý, cũng như triển vọng cho các nghiên cứu tương lai, tạo nên một bước ngoặt trong lịch sử toán học và vật lý.
I. Giới thiệu về Định Lý Descartes và Ý Nghĩa của Nó trong Toán Học Hiện Đại
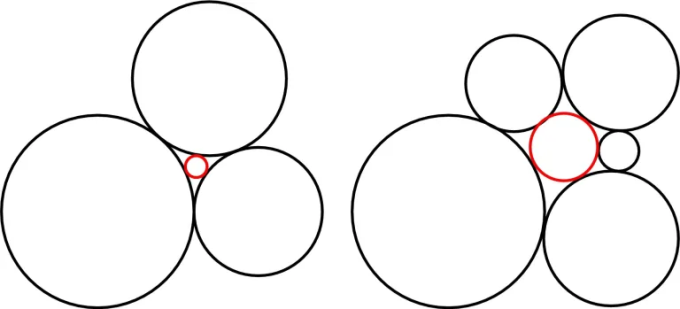
Định lý Descartes, được đặt theo tên nhà toán học và triết gia Pháp René Descartes, đã mang lại nền tảng cho hình học sơ cấp. Định lý này xác định mối liên hệ giữa các bán kính của bốn đường tròn tiếp xúc nhau đôi một. Tuy nhiên, sự quan trọng của Định lý Descartes không chỉ giới hạn trong năm thế kỷ trước mà còn tiếp tục ảnh hưởng đến toán học hiện đại trong nhiều vấn đề chưa được giải quyết.
II. Quá Trình Nghiên Cứu và Những Cải Tiến Mới Nhất từ Đại Học Monash
Gần đây, các nhà nghiên cứu tại Đại học Monash, bao gồm Phó giáo sư Daniel Mathews và nghiên cứu sinh tiến sĩ Orion Zymaris, đã tạo ra những bước ngoặt quan trọng trong việc giải quyết câu đố Descartes. Họ đã phát triển một phương trình tổng quát cho nhiều đường tròn tiếp xúc khác nhau, điều mà các nhà toán học đã tìm kiếm suốt hơn 380 năm.
III. Phương Trình Tổng Quát của Định Lý Descartes: Những Khám Phá và Ứng Dụng
Phương trình tổng quát mà nhóm nghiên cứu phát triển có thể áp dụng cho bất kỳ số lượng đường tròn nào. Đặc biệt, nó mở ra nhiều ứng dụng tiềm năng trong các lĩnh vực như kỹ thuật toán học và nghiên cứu vật lý. Phương trình này đã được công bố trên tạp chí Journal of Geometry and Physics, cho thấy tầm quan trọng của nó trong việc mở rộng hiểu biết của chúng ta về hình học.
IV. Kết Hợp Giữa Toán Học và Vật Lý: Vai Trò của Spinor trong Nghiên Cứu
Các nhà nghiên cứu đã áp dụng các yếu tố vật lý như spinor trong công trình của họ. Spinor là một khái niệm quan trọng trong cơ học lượng tử và thuyết tương đối, giúp tạo ra các mô hình chính xác hơn cho sự tương tác giữa các mô hình hình học. Daniel Mathews nhấn mạnh rằng việc kết hợp giữa toán học và vật lý là chìa khóa để giải quyết các vấn đề mà từ lâu đã bị ràng buộc bởi lý thuyết thông thường.
V. Tác Động của Công Trình Đến Các Vấn Đề Chưa Giải Quyết trong Hình Học
Định lý Descartes đã để lại nhiều câu hỏi chưa được giải đáp trong lịch sử khoa học. Nghiên cứu mới từ Đại học Monash không chỉ giải quyết một trong số những câu hỏi này mà còn mở rộng thêm nhiều hướng nghiên cứu tiếp theo trong hình học. Điều này tạo ra động lực mạnh mẽ cho các thế hệ nhà toán học cao hơn, khuyến khích họ theo đuổi nghiên cứu sâu hơn về toán học hiện đại.
VI. Lịch Sử và Giải Thưởng im Lặng: Thực Tiễn Trong Rộng lớn của Định Lý
Lịch sử của Định lý Descartes đã chứng kiến nhiều nỗ lực không ngừng của các nhà nghiên cứu trên toàn thế giới. Với các khám phá mới từ Đại học Monash, sự chú ý đến các ứng dụng của nó trong hình học đã được khôi phục. Đây không chỉ là một thành tựu cho các nhà nghiên cứu như Daniel Mathews và Orion Zymaris mà còn là một bước đi quan trọng trong việc phân tích và nghiên cứu các hình tròn trong không gian hình học.
VII. Tương Lai của Định Lý Descartes: Triển Vọng Và Cảm Hứng Từ Các Thế Hệ Tiếp Theo
Triển vọng cho Định lý Descartes là rất lớn. Khi mà những công chúa toán học xuyên suốt lịch sử tiếp tục truyền cảm hứng cho các nhà toán học trẻ, họ sẽ tìm cách mở rộng và sáng tạo những tư tưởng của thế hệ đi trước. Điều này cho thấy một tiềm năng không giới hạn cho những nghiên cứu mới trong vật lý và toán học hiện đại, tiếp tục làm phong phú thêm bức tranh lịch sử khoa học.






