Cách hiệu quả phòng bệnh não mô cầu và bảo vệ sức khỏe
Bệnh não mô cầu là một căn bệnh nguy hiểm do vi khuẩn gây ra, có thể dẫn đến những biến chứng nghiêm trọng nếu không được phát hiện và điều trị kịp thời. Trong bài viết này, chúng tôi sẽ cung cấp thông tin chi tiết về nguyên nhân, triệu chứng, nhóm đối tượng có nguy cơ cao, cũng như các biện pháp phòng ngừa hiệu quả và tầm quan trọng của tiêm vaccine. Hãy cùng tìm hiểu để bảo vệ sức khỏe bạn và cộng đồng xung quanh!
1. Định Nghĩa Và Nguyên Nhân Gây Bệnh Não Mô Cầu
Não mô cầu là bệnh do vi khuẩn não mô cầu (Neisseria meningitidis) gây ra, có thể dẫn đến hai biến chứng nghiêm trọng là nhiễm trùng máu và viêm màng não. Bệnh này rất nguy hiểm và có thể gây tử vong trong vòng 24 giờ nếu không được xử lý kịp thời. Vi khuẩn này lây mặc chủ yếu qua đường hô hấp thông qua các hành động như ho, hắt hơi hay chia sẻ thức ăn và đồ uống. Đặc biệt, những người lành mang trùng có thể lây lan bệnh mà không có triệu chứng rõ nét.
2. Các Triệu Chứng Của Nhiễm Não Mô Cầu
Các triệu chứng ban đầu của nhiễm bệnh thường tương tự như cúm bao gồm: sốt, nhức đầu, đau họng, và buồn nôn. Trong 8 giờ đầu, dịch bệnh có thể biểu hiện qua các dấu hiệu như biếng ăn và sổ mũi. Khi bệnh tiến triển, người bệnh có thể gặp:
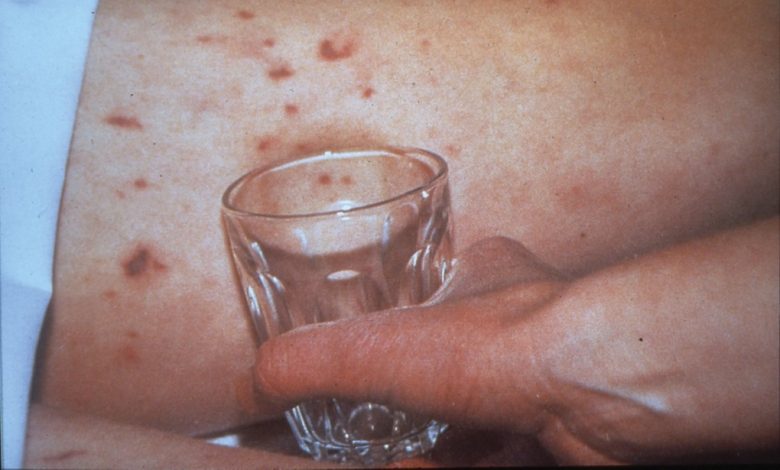
- Tử ban, lạnh tay chân, cứng cổ.
- Hội chứng mê sảng, co giật, có thể dẫn đến hôn mê.
Đối với trẻ sơ sinh, triệu chứng thường gồm tụt sức, bỏ bú và thóp căng phồng.
3. Đối Tượng Có Nguy Cơ Cao Bị Nhiễm Bệnh
Các nhóm người có nguy cơ cao mắc bệnh não mô cầu bao gồm trẻ sơ sinh, thanh thiếu niên, quân nhân, và những người sống trong môi trường tập thể như trường học và ký túc xá. Đặc biệt, người có hệ miễn dịch yếu hoặc hay bị nhiễm trùng đường hô hấp như cúm cũng cần phải đặc biệt cẩn thận.
4. Các Phương Pháp Phòng Ngừa Hiệu Quả
Để giảm thiểu nguy cơ nhiễm bệnh, việc duy trì vệ sinh cá nhân và môi trường sống là vô cùng quan trọng. Các biện pháp nên được áp dụng bao gồm:
- Thường xuyên rửa tay bằng xà phòng.
- Khử khuẩn bề mặt trong nhà, lớp học, và ký túc xá.
- Đeo khẩu trang tại nơi đông người, tránh tiếp xúc gần.
5. Tầm Quan Trọng Của Tiêm Vaccine Trong Phòng Bệnh
Tiêm vaccine là một trong những biện pháp phòng bệnh hiệu quả nhất. Hiện nay, có nhiều loại vaccine ngừa não mô cầu, bao gồm Bexsero, VA-Mengoc BC và Menactra. Những người trong nhóm nguy cơ cao nên chủ động tiêm vaccine để bảo vệ sức khỏe cá nhân và cộng đồng.
6. Vệ Sinh Cá Nhân Và Môi Trường Sống
Cần tăng cường vệ sinh môi trường sống để ngăn chặn sự bùng phát của dịch bệnh. Việc khử khuẩn các bề mặt tiếp xúc thường xuyên và giữ cho không gian sống thông thoáng là rất cần thiết. Ngoài ra, cần chú ý đến những thói quen tốt như không hút thuốc lá và không dùng chung đồ uống với người khác.
7. Vai Trò Của Dinh Dưỡng Và Luyện Tập Thể Thao Trong Bảo Vệ Sức Khỏe
Dinh dưỡng tốt và đủ năng lượng cùng với việc luyện tập thể dục thể thao có thể làm tăng cường hệ miễn dịch, từ đó giúp cơ thể có khả năng chống lại vi khuẩn não mô cầu. Tránh xa thực phẩm có thể gây dị ứng, và duy trì hàm lượng nước trong cơ thể là rất quan trọng.
8. Thực Hành Khử Khuẩn Và Giáo Dục Cộng Đồng
Giáo dục cộng đồng về bệnh não mô cầu và các biện pháp phòng ngừa là rất quan trọng để nâng cao nhận thức và trách nhiệm sức khỏe cộng đồng. Việc thực hành khử khuẩn là cần thiết để bảo vệ bản thân và gia đình.
9. Tham Khảo Ý Kiến Chuyên Gia Và Chương Trình Tiêm Chủng
Người dân nên tham khảo ý kiến các bác sĩ để được tư vấn về chương trình tiêm chủng và các phương pháp thích hợp phòng chống bệnh não mô cầu. Việc này không chỉ bảo vệ sức khỏe cá nhân mà còn góp phần nâng cao sức khỏe cộng đồng.